Data Management (DM)

在PETSc的DM文档中指出，DM 对象用于管理 PETSc 中的代数结构（ Vec 和 Mat ）与基于偏微分方程（或其他）的模拟中的网格数据结构之间的通信，更具体的网格管理由：结构化网格的 DMDA 、交错网格的 DMSTAG 、非结构化网格的 DMPLEX 组成。

DM

DM作为最基本的PETSc代数结构管理器，可以通过下面的代码进行初始化：

dm = PETSc.DM().create(comm=comm)
dm.setType("da")
dm.setFromOptions()
dm.setUp()

其中，setType设置了DM的类型，在DMType文档里可以看到完整的类型列表。

在创建好的DM对象基础上，可以由其管理Vec向量和Mat矩阵的创建，如：

1
2
3

vg = dm.createGlobalVec()
vl = dm.createLocalVec()
A  = dm.createMat()

这里的GlobalVector和LocalVector的区别在于，全局向量是一个并行向量，它不包含 MPI 进程间共享的重复值，也就是说，它没有ghost元素；可以通过globalToLocal和localToGlobal来实现ghost元素的转换。

如果需要短期的使用一个向量，比如在函数中使用，那么可以通过getGlobalVec方法来获取，并且在使用完成后通过restoreGlobalVec返回此向量：

1
2
3

tmp = dm.getGlobalVec(name="tmp")    # or use `getLocalVec`
...
dm.restoreGlobalVec(tmp, name="tmp") # or use `restoreLocalVec`

当离散算子有邻域耦合（有限差分 stencil、有限体积面通量、有限元单元邻接）时，并行边界处的数据交换可以通过DM完成：

DM.globalToLocal(vg, vl, addv=...)：把全局向量更新到带 ghost 的本地向量
DM.localToGlobal(vl, vg, addv=...)：把本地（含 ghost）贡献累加/写回全局向量
DM.localToLocal(vl, vlg, addv=...)：本地向量之间的邻域交换（不经过 global）

总之，在*ToLocal的时候，都会将local的ghost元素进行通信交换。一般来说，只会进行global和local之间的转换：

vl = dm.createLocalVec()
dm.globalToLocal(vg, vl, addv=PETSc.InsertMode.INSERT_VALUES)
# do stencil computing
dm.localToGlobal(vl, vg, addv=PETSc.InsertMode.INSERT_VALUES)

比如下面这段代码：

import sys, petsc4py
petsc4py.init(sys.argv)
from petsc4py import PETSc
import numpy as np

comm = PETSc.COMM_WORLD
rank = comm.getRank()

dm = PETSc.DMDA().create(
    dim=1, sizes=(8,), dof=1,
    stencil_width=1, comm=comm)
dm.setUp()
vl = dm.createLocalVec()

(xs,), (xm,) = dm.getCorners()
(gxs,), (gxm,) = dm.getGhostCorners()
xe, gxe = xs + xm, gxs + gxm

with vl as arr:
    arr[:] = -1.0
    arr[xs-gxs:xe-gxs] = rank * 10 + np.arange(xs, xe)

PETSc.Sys.syncPrint(f"[{rank}]: {vl.getArray()}", comm=comm)
PETSc.Sys.syncFlush(comm=comm)

dm.localToLocal(vl, vl, addv=PETSc.InsertMode.INSERT_VALUES)

PETSc.Sys.syncPrint(f"[{rank}]: {vl.getArray()}", comm=comm)
PETSc.Sys.syncFlush(comm=comm)

其输出结果为：

mpirun -n 2 python test.py
# [0]: [ 0.  1.  2.  3. -1.]
# [1]: [-1. 14. 15. 16. 17.]
# [0]: [ 0.  1.  2.  3. 14.]
 #[1]: [ 3. 14. 15. 16. 17.]

可以看到，localToLocal这个函数，成功将ghost元素进行了交换，并填充到了目标向量中。

最后，DM 直接提供了把回调函数绑上去的接口：

dm.setSNESFunction(function, args=None, kargs=None)：对应 DMSNESSetFunction
dm.setSNESJacobian(jacobian, args=None, kargs=None)：对应 DMSNESSetJacobian
dm.setKSPComputeOperators(operators, args=None, kargs=None)：用于 KSP 的算子装配回调

DMDA

DMDA 面向规则笛卡尔网格的问题（1D/2D/3D 规则划分），它把网格点按规则的 $(i,j,k)$ 方式编号和分块，内置了常用的 stencil（STAR/BOX）和 ghost 点通信；并且DMDA会用这些信息来创建合适布局的向量/矩阵，包括通信与常见的稀疏结构。

在DMDA.pyx源文件中，可以看到DA和DMDA是相同的，这主要是为了兼容旧版本：

1 2	# backward compatibility alias DA = DMDA

常用的接口基本集中在：

da.create(dim, dof, sizes, proc_sizes, boundary_type, stencil_type, stencil_width, ownership_ranges, setup=True)
- dim: 维度数量(1, 2, 3)
- dof: 自由度数量
- sizes: 每个维度的节点数量
- proc_sizes: 每个维度使用的处理器数量
- boundary_type: 边界类型，参见DMBoundaryType文档
- stencil_type: ghost模板的填充类型，参见DMDAStencilType文档
- stencil_width: ghost区域的宽度
- setup: 是否在完成初始创建后，调用setUp()函数，默认是进行调用
- ownership_ranges: 每个处理器上包含的的x,y,z方向的元素数量，其长度等于 proc_sizes，并且在各方向上求和等于 sizes
- comm: MPI communicator, 默认值为 PETSc.Sys.getDefaultComm
da.getCorners() / DMDA.getGhostCorners()
- 本 rank 拥有区域与 ghost 区域
da.getVecArray(vec, readonly=False)
- 把 Vec 暴露成 N 维数组视图，支持 with
da.setUniformCoordinates(xmin,xmax, ymin,ymax, ...)
- 设置坐标，方便 view/VTK 输出
da.getAO()
- 自然序与PETSc内部序的映射，做矩阵装配时常见

DMBoundaryType

在DMDA的create方法中，可以传入一个boundary_type的参数，用来定义DMBoundaryType文档中给出的不同类型的边界条件，类型如下：

DMBoundaryType	说明
`DM_BOUNDARY_NONE`	无ghost节点，是默认情况（只有通过`stencil`实现的处理器之间的ghost）
`DM_BOUNDARY_GHOSTED`	存在但未填充的ghost节点，用户可以向其中赋值，然后应用使用这些ghost位置的stencil
`DM_BOUNDARY_MIRROR`	ghost节点的值与第一个网格点的值相同（the same as the value 1 grid point in），也就是说，真实网格中的第0个网格点起到镜像作用，用于定义ghost节点的值，尚未在3D网格中实现
`DM_BOUNDARY_PERIODIC`	由域（domain）的相对边缘（opposite edge）填充的ghost节点，实现周期边界
`DM_BOUNDARY_TWIST`	类似于周期性，只是像莫比乌斯带（Mobius strip）一样反向粘合

注意，这是物理域边界的信息。它与处理器之间的边界无关，并且该宽度始终由模板宽度（stencil_width）决定。

下面的结果演示中，总长度为8，使用4个处理器分组，并把boundary设置为-1，以及内部点设置为处理器的rank大小，而处理器之间的ghost会根据*ToLocal函数进行填充。下面的结果显示，对于rank=1,2这两个内部处理器，其左右两侧的ghost节点是分别由rank=0,3传递过来的，因此主要问题是关注rank=0的左侧ghost节点以及rank=3的右侧ghost节点。

对于Dirichlet边界条件，可以采用PETSc.DM.BoundaryType.NONE实现。可以看到，rank=0没有左侧ghost节点，而rank=3没有右侧ghost节点，可以进行Dirichlet边界条件的填充。其结果如下：

[NONE (Dirichlet) ] Rank 0 | GRange=[ 0: 3] | Array: [   0, 0, 1]
[NONE (Dirichlet) ] Rank 1 | GRange=[ 1: 5] | Array: [0, 1, 1, 2]
[NONE (Dirichlet) ] Rank 2 | GRange=[ 3: 7] | Array: [1, 2, 2, 3]
[NONE (Dirichlet) ] Rank 3 | GRange=[ 5: 8] | Array: [2, 3, 3   ]

对于Neumann边界条件，可以采用PETSc.DM.BoundaryType.GHOSTED实现。左右两侧的边界点都存在，并且在 *ToLocal函数时不会被填充，需要用户自己指定。其结果如下：

[GHOSTED (Neumann)] Rank 0 | GRange=[-1: 3] | Array: [-1, 0, 0,  1]
[GHOSTED (Neumann)] Rank 1 | GRange=[ 1: 5] | Array: [ 0, 1, 1,  2]
[GHOSTED (Neumann)] Rank 2 | GRange=[ 3: 7] | Array: [ 1, 2, 2,  3]
[GHOSTED (Neumann)] Rank 3 | GRange=[ 5: 9] | Array: [ 2, 3, 3, -1]

对于特殊的Neumann边界条件，即法向梯度为0, 可以用PETSc.DM.BoundaryType.MIRROR实现，它会把左右的边界点复制一遍到ghost节点处：

[MIRROR] Rank 0 | GRange=[-1: 3] | Array: [0, 0, 0, 1]
[MIRROR] Rank 1 | GRange=[ 1: 5] | Array: [0, 1, 1, 2]
[MIRROR] Rank 2 | GRange=[ 3: 7] | Array: [1, 2, 2, 3]
[MIRROR] Rank 3 | GRange=[ 5: 9] | Array: [2, 3, 3, 3]

对于Period边界条件，可以采用PETSc.DM.BoundaryType.PERIODIC实现。左右两侧的ghost节点，通过*ToLocal函数，把实际的内点赋值过来，实现了周期边界条件。其结果如下：

[PERIODIC] Rank 0 | GRange=[-1: 3] | Array: [3, 0, 0, 1]
[PERIODIC] Rank 1 | GRange=[ 1: 5] | Array: [0, 1, 1, 2]
[PERIODIC] Rank 2 | GRange=[ 3: 7] | Array: [1, 2, 2, 3]
[PERIODIC] Rank 3 | GRange=[ 5: 9] | Array: [2, 3, 3, 0]

DMDAStencilType

在DMDAStencilType文档中，给出了DMDA中的stencil_type的取值情况，如下所示：

DMDAStencilType	说明
`DMDA_STENCIL_STAR`	只沿着坐标方向进行延伸；即在逻辑网格坐标中，只有 $(i,j,k),(i+s,j,k),(i,j+s,k),(i,j,k+s)$ 位于模板内，但例如$(i+s,j+s,k)$不包含在内
`DMDA_STENCIL_BOX`	除了坐标方向的延伸，还沿着四个方向角方向进行延伸；即在逻辑网格坐标系中，$(i,j,k), (i+s,j+r,k+t)$ 中的任何一个都可以位于模板内

Corners/GhostCorners

getCorners() 返回本 rank 拥有的那块子域的全局索引与尺寸（不含 ghost），而getGhostCorners() 返回带 ghost 的子域范围（含邻居数据）。

# owned region: i in [xs, xs+xm), j in [ys, ys+ym)
(xs, ys),   (xm, ym)   = da.getCorners()
# ghost region: i in [gxs, gxs+gxm), j in [gys, gys+gym)
(gxs, gys), (gxm, gym) = da.getGhostCorners()

getVecArray

getVecArray(vec, readonly=<true|false>) 返回的是一个数组视图对象，它内部会根据 Vec 的 local size 判断这是 global vector（不含 ghost）还是 local vector（含 ghost），然后给出相应形状。它还实现了 __enter__/__exit__，所以可以使用with ... as语法糖进行调用：

vec = da.createLocalVec()
with da.getVecArray(vec, readonly=True) as va:
  ...
  # va: (x, y, z, dof)
  # `va.array` is `numpy.ndarray` object

注意，使用DMDA的vector array, 和Vec对象有一些不同，其中：

轴顺序是 x 在前：也就是说二维时用 a[i, j]，不是 a[j, i]。这和它的自然编号（x 最快，其次 y）一致
使用全局索引访问本地数组：DMDA的vector会用本 rank 的起点 (xs,ys,...) 做偏移调整，所以在 owned 区域内，可以直接写 a[i, j]（这里的 i,j 是全局网格索引），不需要手动减去 xs,ys

DMPlex

DMPlex 面向非结构网格/一般网格（三角形、四面体、混合单元等），它用一种通用的拓扑表示来描述网格，表达单元、面、边、点之间的连接关系，然后再把自由度如何放到这些网格点上的问题，交给 PetscSection 等机制管理。因此，DMPlex适合有限元、非结构网格有限体积等做法。在DMPlex.pyx文档中，给出了常用函数：

生成网格：createBoxMesh(...)
读拓扑范围：getChart()、getDepth()、getDepthStratum(d)、getHeightStratum(h)
网格处理：symmetrize()、interpolate()、distribute()
视图与 options：setFromOptions()、view()

DMPlex把网格看成一个 DAG（点(point)有 cone，即向下连的点，比如 cell 的顶点/边/面；也有 support，即向上被谁引用），从而方便网格的管理。

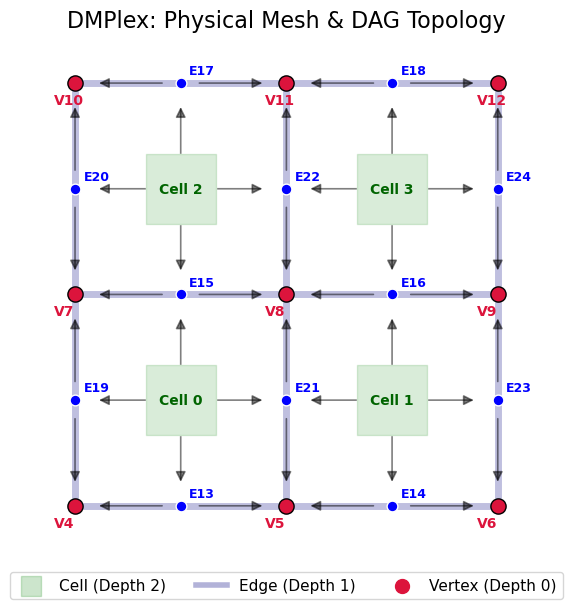
DMPlex的createBoxMesh函数，其函数签名为：

createBoxMesh(self,
  faces: Sequence[int],
  lower: Sequence[float] | None = (0, 0, 0),
  upper: Sequence[float] | None = (1, 1, 1),
  simplex: bool | None = True,
  periodic: Sequence | str | int | bool | None = False,
  interpolate: bool | None = True,
  localizationHeight: int | None = 0,
  sparseLocalize: bool | None = True,
  comm: Comm | None = None) -> Self

其中：

faces：每个空间维度上的面（cells）数量；如果为 None，则使用默认值
lower：计算区域的左下角坐标
upper：计算区域的右上角坐标
simplex：是否使用单纯形单元：
- True 表示使用单纯形（simplices, 1D 为线段，2D 为三角形，3D 为四面体）
- False 表示使用张量积单元（tensor cells, 2D 为四边形，3D 为六面体）
periodic：X、Y、Z 方向上的边界类型；如果为 None，则等价于 DM.BoundaryType.NONE（非周期边界）
interpolate：是否创建中间维度的网格实体，例如边(edges)、面(faces)。
localizationHeight：是否在单元(cells)之外，对边(edges)、面(faces)也进行局部化处理；该参数只在周期网格中有意义。
sparseLocalize：是否只对靠近周期边界的单元进行坐标局部化；该参数只在周期网格中有意义。
comm: MPI communicator, 默认值为 PETSc.Sys.getDefaultComm

如果要更深入的使用PETSc的FEM功能，可以参考FE.pyx源文件中的内容。

Poisson equation

下面考虑在一个2D正方形$[0,1]\times [0,1]$上求解泊松方程：
$$
-\nabla^2 u=f
$$
边界条件设置为$u|_{\partial \Omega}=0$，构造了人造解 $u(x,y)=\sin(\pi x)\cdot \sin(\pi y)$，满足：

$$
f(x,y)=2\pi^2 \cdot \sin(\pi x) \cdot \sin(\pi y)
$$
考虑弱形式：
$$
\begin{align}
& -\nabla^{2}u=f \\
\implies & -\int w\cdot \nabla^{2}u , d\Omega=\int w\cdot f , d\Omega \\
\implies & \int \nabla w\cdot \nabla u , d\Omega -\int {\partial\Omega} \nabla u\cdot n , dS=\int w\cdot f , d\Omega \\
\implies & \int \nabla w\cdot \nabla u , d\Omega=\int w \cdot f , d\Omega
\end{align}
$$
选择Q1基函数展开，得到：
$$
\begin{cases}
KU=F \\
K{ij}=\int \nabla N_{i} \cdot \nabla N_{j} d\Omega \\
F_{i}=\int N_{i} \cdot f d\Omega
\end{cases}
$$
代码如下：

import sys, petsc4py; petsc4py.init(sys.argv)
from petsc4py import PETSc; import numpy as np

# setup
opt   = PETSc.Options()
n     = opt.getInt("nx", 50)
u_ex  = lambda x: np.sin(np.pi*x[0]) * np.sin(np.pi*x[1])
f_rhs = lambda x: 2 * np.pi**2 * u_ex(x)

# DMPlex (Q1 elements)
dm = PETSc.DMPlex().createBoxMesh(faces=(n, n), simplex=False)
dm.setField(0, PETSc.FE().createLagrange(
    dim=2,             # 2D
    nc=1,              # scalar field
    isSimplex=False,   # tensor cells
    k=1,               # Q1
    qorder=1,          # quadrature order
))
dm.createDS()          # create discrete systems
dm.distribute()
dm.setUp()

# basis functions
fe, _ = dm.getField(0)
points, weights = fe.getQuadrature().getData()
points = points.reshape(-1, 2)
V_inv = np.linalg.inv([[1, x, y, x*y] for x,y in [[-1,-1],[1,-1],[1,1],[-1,1]]])
basis = [(np.array([1,p[0],p[1],p[0]*p[1]]) @ V_inv,
          np.array([[0, 1, 0, p[1]],
                    [0, 0, 1, p[0]]]) @ V_inv)
         for p in points]

# assemble
A     = dm.createMatrix()
b     = dm.createGlobalVec()
uex   = b.duplicate()
u     = b.duplicate()
bl    = dm.createLocalVec()
ul    = dm.createLocalVec()
c_sec = dm.getCoordinateSection()
c_loc = dm.getCoordinatesLocal()
ADD   = PETSc.InsertMode.ADD_VALUES
INS   = PETSc.InsertMode.INSERT_VALUES

for c in range(*dm.getHeightStratum(0)):
    v = dm.getVecClosure(c_sec, c_loc, c).reshape(-1, 2)
    Ke = np.zeros((4, 4))
    Fe = np.zeros(4)
    for q, (N, dNr) in enumerate(basis):
        J   = dNr @ v
        det = abs(np.linalg.det(J)) * weights[q]
        dNp = np.linalg.inv(J).T @ dNr
        Ke += (dNp.T @ dNp) * det
        Fe += N * f_rhs(N @ v) * det
    dm.setMatClosure(None, None, A, c, Ke.flatten(), addv=ADD)
    dm.setVecClosure(None, bl, c, Fe, addv=ADD)
    dm.setVecClosure(None, ul, c, [u_ex(p) for p in v], addv=INS)

dm.localToGlobal(bl, b, addv=ADD)
dm.localToGlobal(ul, uex, addv=INS)
A.assemble()
b.assemble()

# boundary conditions
dm.markBoundaryFaces('marker', 1)
dm.labelComplete(dm.getLabel('marker'))
lbl = dm.getLabel('marker')
bc = [dm.getPointGlobal(v)[0]
        for v in range(*dm.getDepthStratum(0)) 
        if lbl.getValue(v)==1 and dm.getPointGlobal(v)[0]>=0]
A.zeroRowsColumns(PETSc.IS().createGeneral(bc), diag=1.0, b=b, x=uex)

# solve
ksp = PETSc.KSP().create()
ksp.setOperators(A)
ksp.setFromOptions()
ksp.solve(b, u)

# error analysis
err = (u-uex).norm(PETSc.NormType.NORM_INFINITY)
PETSc.Sys.Print(f"|u-uex|_inf = {err:.2e}")