0x00 2021新高考
已知函数 $m(x)=x(1-\ln x)$
设 $a,b$ 为两个不相等的正数, 且 $b\ln a-a \ln b=a-b$, 证明 $2 < \frac{1}{a}+\frac{1}{b} < e$
$b \ln a-a \ln b=a-b \Rightarrow \frac{1+\ln b}{b}=\frac{1+\ln a}{a}$
不妨设 $0<a<b,t=\frac{a}{b} \in (0,1)$, 则有 $a=bt,\frac{1+\ln b}{b}=\frac{1+\ln (bt)}{bt}$
故 $t(1+\ln b)=1+\ln b + \ln t \Rightarrow \ln b=\frac{1+\ln t-t}{t-1} \Rightarrow b=e^{\frac{\ln t}{t-1}-1} \Rightarrow a=bt=te^{\frac{\ln t}{t-1}-1}$
所以 $\frac{1}{a}+\frac{1}{b}=\frac{1}{b}(\frac{1}{t}+1)=e^{1-\frac{\ln t}{t-1}}\frac{t+1}{t}$
不妨设 $f(t)=\frac{t+1}{t}e^{1-\frac{\ln t}{t-1}}$, 考虑到 $\lim_{t \to 1}f(t)=2,\lim_{t \to 0}f(t)=e$, 下证 $f(t)$ 在 $(0,1)$ 单调递减
$$
\begin{align}
f’(t)
&=(-\frac{1}{t^2})e^{1-\frac{\ln t}{t-1}}+\frac{t+1}{t}(-\frac{\frac{t-1}{t}-\ln t}{(t-1)^2})e^{1-\frac{\ln t}{t-1}} \\
&=e^{1-\frac{\ln t}{t-1}}\left( -\frac{1}{t^2}-\frac{(t+1)(\frac{t-1}{t}-\ln t)}{t(t-1)^2} \right) \\
&=-e^{1-\frac{\ln t}{t-1}}\left( \frac{\frac{(t-1)^2}{t}+(t+1)(\frac{t-1}{t}-\ln t)}{t(t-1)^2} \right) \\
&=-e^{1-\frac{\ln t}{t-1}}\left( \frac{\frac{t^2+1-2t}{t}+\frac{t^2-1}{t}-(t+1)\ln t}{t(t-1)^2} \right) \\
&=-e^{1-\frac{\ln t}{t-1}}\left( \frac{2t-2-(t+1)\ln t}{t(t-1)^2} \right) \\
\end{align}
$$
由对数均值不等式得 $\frac{t-1}{\ln t} \le \frac{t+1}{2}$, 故 $(t+1)\ln t \le 2(t-1)$, 故 $2t-2-(t+1)\ln t \ge 0$
所以 $f’(t) \le 0$, 即 $f(t)$ 在 $(0,1)$ 单调递减
故 $2=f(0) < f(t) < f(1)=e(0<t<1)$, 得证
0x01 2020全国I
已知函数 $f(x)=e^x+ax^2-x$
当 $x \ge 0$ 时, $f(x) \ge \frac{1}{2}x^3+1$, 求 $a$ 的取值范围
当 $x=0$ 时, $a \in \mathbb{R}$
考虑分离参变量, 即 $a \ge \frac{\frac{x^3}{2}+x+1-e^x}{x^2}(x>0)$
设 $h(x)=\frac{\frac{x^3}{2}+x+1-e^x}{x^2}(x>0)$
$$
\begin{align}
h’(x)
&= \frac{(\frac{3x^2}{2}+1-e^x)x-x^3-2x-2+2e^x}{x^3} \\
&= \frac{e^x(2-x)+\frac{x^3}{2}-x-2}{x^3} \\
&= \frac{(2-x)(e^x-\frac{x^2}{2}-x-1)}{x^3} \\
\end{align}
$$
而 $e^x \ge 1+x+\frac{x^2}{2}$, 故 $h’(x)$ 在 $(0,2)$ 单调增, 在 $(2,\infty)$ 单调递减
所以 $h(x) \le h(2)=\frac{7-e^2}{4},a \ge h(x) \Rightarrow a \ge \frac{7-e^2}{4}$
0x02 斜率方程
$$
\begin{equation}
\begin{cases}
y=kx+m \\
\frac{x^2}{a^2}+\frac{y^2}{b^2}=1
\end{cases}
\end{equation}
\Rightarrow
(b^2+a^2k^2)x^2+2a^2kmx+a^2m^2-a^2b^2=0
$$$$
\begin{equation}
\begin{cases}
m(x-x_0)+n(y-y_0)=1 \\
\frac{x^2}{a^2}+\frac{y^2}{b^2}=1 \\
k=\frac{y-y_0}{x-x_0}
\end{cases}
\end{equation} \\
\Rightarrow
\frac{1+2y_0n}{b^2}k^2+(\frac{2x_0n}{a^2}+\frac{2y_0m}{b^2})k+\frac{1+2x_0m}{a^2}=(1-\frac{x_0^2}{a^2}-\frac{y_0^2}{b^2})(m^2+n^2k^2+2mnk)
$$$$
\begin{equation}
\begin{cases}
mx+ny=1 \\
\frac{x^2}{a^2}+\frac{y^2}{b^2}=1 \\
k=\frac{y}{x}
\end{cases}
\end{equation}
\Rightarrow
\frac{1}{b^2}k^2+\frac{1}{a^2}=m^2+n^2k^2+2mnk
$$
考虑椭圆 $\tau:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$,在平面内有一点 $P(x_0,y_0)$,同时设直线 $l:m(x-x_0)+n(y-y_0)=1$ 与 $\tau$ 相交于点 $A(x_1,y_1),B(x_2,y_2)$
联立 $\tau,l$ 可得:
$$
\frac{1+2y_0n}{b^2}k^2+\left(\frac{2x_0n}{a^2}+\frac{2y_0m}{b^2}\right)k+\frac{1+2x_0m}{a^2}=\left(1-\frac{x_0^2}{a^2}-\frac{y_0^2}{b^2}\right)\left(m^2+n^2k^2+2mnk\right)
$$
其中 $k=\frac{y-y_0}{x-x_0}$
下面考虑 $P$ 在 $\tau$ 上的情况
斜率之和为定值
$$
\begin{aligned}
&k_1+k_2=\lambda \\
&-\frac{\frac{2x_0n}{a^2}+\frac{2y_0m}{b^2}}{\frac{1+2y_0n}{b^2}}=\lambda \\
&\frac{2x_0n}{a^2}+\frac{2y_0m}{b^2}+\lambda\frac{1+2y_0n}{b^2}=0 \\
&m=-\left(\frac{2x_0n}{a^2}+\lambda\frac{1+2y_0n}{b^2}\right) \frac{b^2}{ 2 y _ 0} \\
&m=-n\left(\lambda+\frac{b^2x_0}{a^2y_0}\right)-\frac{\lambda}{ 2 y _ 0} \\
&l:\left[-n\left(\lambda+\frac{b^2x_0}{a^2y_0}\right)-\frac{\lambda}{ 2 y _ 0}\right](x-x _ 0)+n(y-y_0)=1 \\
&l:n\left[\left(\lambda+\frac{b^2x_0}{a^2y_0}\right)(x_0-x)+(y-y_0)\right]+\frac{\lambda}{ 2 y _ 0}(x _ 0-x)=1
\end{aligned}
$$
故过定点 $\left(x_0-y_0\cdot\frac{2}{\lambda},y_0-y_0\cdot\frac{2}{\lambda}\right)$
特别的,当 $\lambda=0$ 时,有 $l:n\left[\frac{b^2x_0}{a^2y_0}(x_0-x)+(y-y_0)\right]=1,k_l=\frac{b^2x_0}{a^2y_0}$
斜率之积是定值
鸽了
斜率之比是定值
鸽了
0x03
当 $n \rightarrow 0$, 或许有 $\frac{x^{2n}-1}{x^{2n}+1}= \ln x =\frac{x^{2n}-1}{2nx^n}$
0x04
$e^x \ge a\ln x + (\ln a) \cdot \frac{e^x}{x}$ 在 $x>0$ 恒成立, 求 $a$ 范围
$0 < a \le 1$
$e^x \ge \ln x \ge a\ln x + (\ln a) \frac{e^x}{x}$
$a \gt 1$
$a \ln x +(\ln a) \cdot \frac{e^{x}}{x} \ge (\ln a)\frac{e^x}{x}$
取 $x= \ln a$,得 $(\ln a)a/\ln a=a>\ln a$,故而 $a >1$ 时原式不成立
综上,$0 < a \le 1$
0x05
现在有一个神奇的机器, 一开始上面显示数字 $k$,每按下一次按钮,数字会等概率变成 $[0,k)$ 之间的一个整数
显然操作有限次它会变成 $0$, 求:数字 $n$ 在这一过程中出现的概率
不妨设 $G_k(x)$ 为所求概率生成函数
显然有 $G_{k+1}(x)=G_k(x) \cdot \frac{k}{k+1} + G_k(x) \cdot \frac{1}{k+1} + \frac{x^k}{k+1}=G_k(x)+\frac{x^k}{k+1}$
故:
$$
p(n)=\begin{cases}
&1 &n=k \\
&\frac{1}{k+1} &0 \le n < k \\
&0 & n>k
\end{cases}
$$
0x06
$$
\begin{aligned}
& \frac{k_1}{k_1^2-3}+\frac{k_2}{k_2^2-3}=0 \\
& \frac{k_1}{k_1^2-3}=\frac{-k_2}{(-k_2)^2-3} \Rightarrow k_1=-k_2 \\
let: \,\, &\frac{x}{x^2-3}=w \\
then:\,\, & wx^2-x-3w=0 \\
therefore: \,\, & k_1 \cdot (-k_2)=\frac{-3w}{w}=-3 \Rightarrow k_1 \cdot k_2=3
\end{aligned}
$$
或者:
$$
\begin{align}
& another \, story. \\
& k_1-\frac{3}{k_1}=-(k_2-\frac{3}{k_2}) \\
& k_1+k_2=3\frac{k_1+k_2}{k_1k_2} \\
so \,\, & k_1+k_2=0 \,\,\,\, or \,\,\,\,k_1k_2=3
\end{align}
$$
0x07 质子守恒
下面只考虑同簇酸根溶液的质子守恒
设有某 $n$ 元酸 $H_nA$,且有一溶液中 $[H_kA^{(n-k)-}]=c_k$
现将所有酸根拆分成 $H^+,A^{-}$ 形式,假设 $H^+$ 等价总浓度 $c_H$,且 $A^{-}$ 等价总浓度 $c_A$
由得失质子守恒,可得:
$$
c_H=[H^+]+\sum_{k=1}^{n}k[H_kA^{(n-k)-}]
$$
0x08
$$
0<a<\frac{e}{4},proof:2a+2a\ln x < \frac{e^x}{x}(x>0)
$$
法一: $2a(1+\ln x) < 2ax<\frac{ex}{2}<\frac{e^x}{x}$
法二: 当 $0<x<1$ 时,即证 $2a<\frac{e^x}{x}+a\ln \frac{1}{x}$
由于 $2a<\frac{e}{2}$ 且 $\frac{e^x}{x}+a\ln \frac{1}{x}>\frac{e^x}{x}>\frac{ex}{x}=e>\frac{e}{2}$
所以 $0<x<1$ 时原命题成立
当 $x \ge 1$ 时,有 $2a+2a\ln x<\frac{e}{2} + \frac{e}{4} \ln x$
即证 $\frac{e}{2} + \frac{e}{4} \ln x < \frac{e^x}{x}$
即证 $2 + \ln x < \frac{4e^{x-1}}{x}$
由于 $2+\ln x \le 2+x-1=x+1$
即证 $x^2+x \le 4e^{x-1}$
设 $h(x)=4e^{x-1}-x^2-x$,则有 $h’(x)=4e^{x-1}-2x-1,h’’(x)=4e^{x-1}-2 \ge h’’(1)=2 > 0(x \ge 1)$
因此 $h’(x)$ 在 $(1,\infty)$ 单调递增,故而 $h’(x) \ge h’(1)=3>0$
因此 $h(x)$ 在 $(1,\infty)$ 单调递增,故而 $h(x) \ge h(1)=2>0$
所以 $x \ge 1$ 时原命题成立
综上,原命题成立
0x09
$$
(ka+1)(kb+1)=k(a+b+kab)
$$
0x0A
$$
\begin{align}
& \ln x-x+\sin x+a=0 (1<a<3)\\
& 设 h(x)=\ln x - x + \sin x \\
& 当 x > 6,h(x) \le \ln x- x + 1 < -3\\
& 由于 6 < 2\pi,所以只需要考虑 0<x<2\pi 上的情况 \\
& 易得:
\end{align}
$$
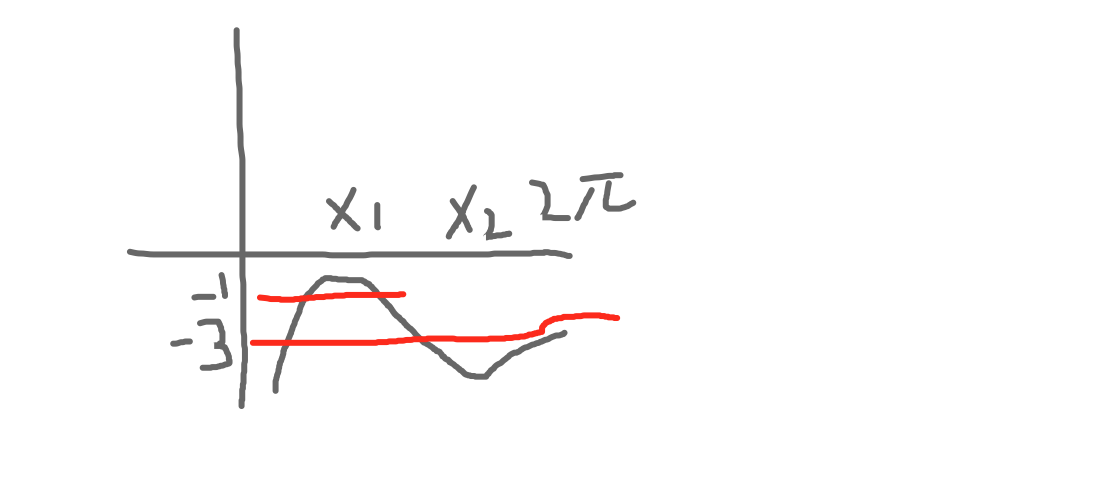
| $x$ | $(0,x_1)$ | $(x_1,\pi)$ | $(\pi,\frac{3}{2}\pi)$ | $(\frac{3}{2}\pi,x_2)$ | $(x_2,2\pi)$ |
|---|---|---|---|---|---|
| $h(x)$ | $\nearrow$ | $\searrow$ | $\searrow$ | $\searrow$ | $\nearrow$ |
$而 h’(1)=\cos 1>0,h(1)=-1+\sin 1>-1,故0<1<x_1$
$又因为 h(6)<-3,h(x_2)<h(6),h(2\pi)<-3,所以有:$
$$
\begin{cases}
&h(0^{+}) \to -\infty \\
&h(x_1)>-1 \\
& h(x_2)<-3 \\
& h(2\pi)<-3 \\
\end{cases}
$$
$y=h(x)图像大致为:$
0x0B 转自知乎
证明 $y=\sin\sqrt x$ 不是周期函数
假设有周期 $T$
则 $\sin 0 = \sin \sqrt T=\sin \sqrt{2T}$
从而 $\sqrt T=k_1 \pi,\sqrt{2T}=k_2 \pi (k_1,k_2 \in \mathbb{Z})$
则有 $\frac{k_1}{k_2} =\frac{\sqrt 2}{2} \not\in \mathbb{R}$
与 $\frac{k_1}{k_2} \in \mathbb{R}$ 矛盾,故假设不成立,原函数不存在周期
0x0C
$$
\begin{align}
&\lim_{x \to 1} \frac{x^3-1}{\sqrt{2x+2}-2} \\
=&\lim_{x \to 1} \frac{(x-1)(x^2+x+1)}{\sqrt{2x+2}-2} \\
=&\lim_{x \to 1} \frac{(x-1)(x^2+x+1)(\sqrt{2x+2}+2)}{2x+2-4} \\
=&\lim_{x \to 1} \frac{(x-1)(x^2+x+1)(\sqrt{2x+2}+2)}{2(x-1)} \\
=&\lim_{x \to 1} \frac{(x^2+x+1)(\sqrt{2x+2}+2)}{2} \\
=&\frac{3 \cdot 4}{2} \\
=&6
\end{align}
$$
$$
\begin{align}
&\lim _ {x \to \infty} (\frac{x ^ 2}{x+1}-ax) \\
=&\lim _ {x \to \infty} (\frac{x ^ 2-ax(x+1)}{x+1}) \\
=&\lim _ {x \to \infty} (\frac{(1-a)x ^ 2-ax}{x+1}) \\
\text{if a>0} \\
&\lim _ {x \to \infty} (\frac{x^2}{x+1}-ax) \\
=&\lim _ {x \to \infty} (\frac{(x+1) ^ 2-2(x+1)-1+2}{x+1}-ax) \\
=&\lim _ {x \to \infty} (x+1-2+\frac{ 1 }{x+1}-ax) \\
=&\lim _ {x \to \infty} (x+1-2-ax) \\
=&\lim _ {x \to \infty} ((1-a)x-1) \\
& \text{当且仅当} a=1 \text{时存在有理极限}
\end{align}
$$
