三元环计数

万恶之源：

给定一张无重边、无自环的无向图

点数为$n$，边数为$m$，且$n,m$同阶

问有多少个无序三元组$(i,j,k)$，使得存在：

1. 有一条连接$i,j$的边
2. 有一条连接$j,k$的边
3. 有一条连接$k,i$的边

举个例子：

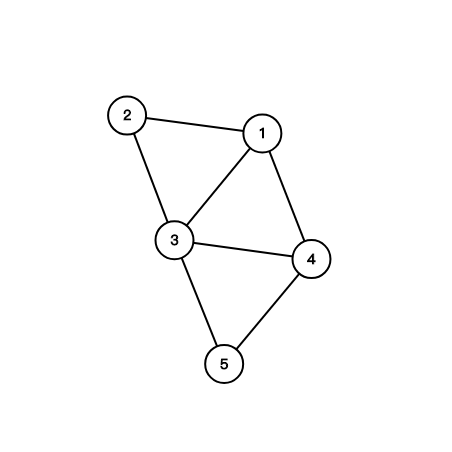
这张图中有三个三元环：$(1,2,3),(1,3,4),(3,4,5)$

---

有一个显然的基于度数的乱搞的做法（本人并没有写过……），可以在这里阅读到：jiachin_zhao 三元环计数

这里介绍一种十分优秀的三元环计数方法：

首先要对所有的无向边进行定向，对于任何一条边，从度数大的点连向度数小的点，如果度数相同，从编号小的点连向编号大的点

此时这张图是一个有向无环图

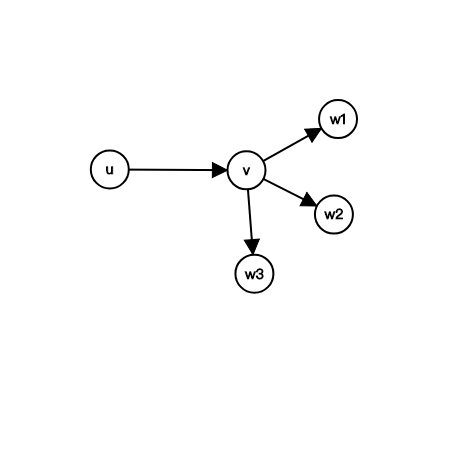
之后枚举每一个点$u$，然后将$u$的所有相邻的点都标记上“被$u$访问了”，然后再枚举$u$的相邻的点$v$，然后再枚举$v$的相邻的点$w$，如果$w$存在“被$u$访问了”的标记，那么$(u,v,w)$就是一个三元环了

而且每个三元环只会被计算一次

---

那么现在就只需要证明三件事：

1. 定向后的图是一个有向无环图

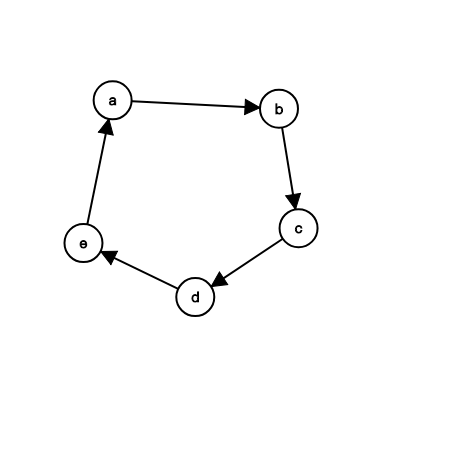
以上图为例，用$deg_u$表示$u$在原图中的度数，则$deg_a \ge deg_b \ge deg_c \ge deg_d \ge deg_e \ge deg_a$

既$deg_a=deg_b=deg_c=deg_d=deg_e=deg_a$

对于度数相同的点，是按照编号从小到大连边的，则$a \le b \le c \le d \le e \le a$

既$a=b=c=d=e$

然而点的编号是$1 \sim n$的全排列，因此不会产生如上的事情，既不存在环

由于这张图有向，而且没有环，因此这张图就是有向无环图

2. 时间复杂度是$O(m \sqrt m)$（在此认为$n,m$同阶）

对于“打标记”这个操作，每个点都会将所有的出边遍历一遍，那么这里的时间复杂度为$O(n+m)$

对于访问$u$，然后访问$v$，然后访问$w$，可以这么考虑：对于每条边（$u \rightarrow v$），对时间复杂度的贡献为$out_v$，其中$out_v$表示$v$的出边个数

这样就转化为了求$\sum_{i=1}^{n}out_i$

不妨将$out_v$分类讨论

1. $out_v \le \sqrt m$，那么由于$u$连接$v$，因此$deg_u \ge deg_v$，这样的$u$的个数是$O(n)$的，因此这里的时间复杂度为$O(n \sqrt m)$
2. $out_v \gt \sqrt m$，那么由于$u$连接$v$，因此$deg_u \ge deg_v$，既$deg_u \gt \sqrt m$，这样的$u$的个数是$O(\sqrt m)$的，因此这里的时间复杂度为$O(\sqrt m m)=O(m \sqrt m)$

因此时间复杂度为$O(n+m+n\sqrt m+m\sqrt m)=O(m \sqrt m)$

3. 每个三元环只会被统计一次

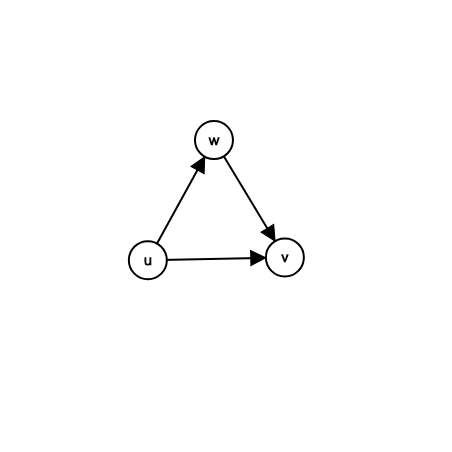
三元环在有向无环图上无非就长这样：

也只能且只会在$u$处被计算一次

---

事实上连边的时候从度数小的连向度数大的也可以证明时间复杂度是$O(m \sqrt m)$……

---

下面是一个样例程序

#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
vector<int> g[N];
int deg[N], vis[N], n, m, ans;
struct E { int u, v; } e[N * 3];
int main() {
    scanf("%d%d", &n, &m);
    for(int i = 1 ; i <= m ; ++ i) {
        scanf("%d%d", &e[i].u, &e[i].v);
        ++ deg[e[i].u], ++ deg[e[i].v];
    }
    for(int i = 1 ; i <= m ; ++ i) {
        int u = e[i].u, v = e[i].v;
        if(deg[u] < deg[v] || (deg[u] == deg[v] && u > v)) swap(u, v);
        g[u].push_back(v);
    }
    for(int x = 1 ; x <= n ; ++ x) {
        for(auto y: g[x]) vis[y] = x;
        for(auto y: g[x])
            for(auto z: g[y])
                if(vis[z] == x)
                    ++ ans;
    }
    printf("%d\n", ans);
}

---

一些习题